Learn these four models first for time-series forecasting
including applications in economics and finance, as well as the Python packages to implement them
Today, we are spoiled for choice in terms of tools and models for forecasting. You might be tempted to dive straight into machine learning and neural networks for a time-series prediction problem.
However, such techniques can often be overkill—you might end up with an overly complex model that cannot be explained to decision-makers or is completely unsuited to your dataset.
I’ll walk you through four classical time series models that excel in interpretability and their ability to provide insights into economic or financial patterns. These models prioritize clarity over pure predictive accuracy, breaking predictions into coefficients that clearly show each variable's impact.
Many of these models are the bread and butter of practitioners working with economic and financial data. They can be used to forecast everything from GDP to stock prices to electricity demand.
I’ll provide a high-level overview of each model, a glimpse of some real-world applications, and the Python packages to implement them. There will be handy links to practical Python guides throughout if you want to dive deeper.
Autonomous Econ aims to empower analysts who work with economic data by equipping them with Python and data science skills.
Posts will largely center on practical guides but will also include data journalism pieces from time to time.
Subscribe and join 2.7k+ others to work smarter through automation and become a savvier analyst.
The principles of time series forecasting
Time series data refers to a dataset in which each data point corresponds to a specific point in time. This means that each observation cannot be treated independently, as the time dimension adds an explicit order to the data.
Forecasting time series data involves using historical data to predict future values. This process requires identifying patterns in the data to make accurate predictions.
When predicting a variable (Y), these patterns can be broken down into the following components:
Y = level + trend + seasonality + noiseYou can easily vizualise these components with Python using seasonal_decompose from statsmodels.
import statsmodels.api as sm
# Perform seasonal decomposition
decomposition = sm.tsa.seasonal_decompose(
cpi_monthly_pct_change, model="additive", period=12
)
# Plot the decomposed components
fig = decomposition.plot()These decompositions give us a first impression and help us decide what assumptions to use when building a model. Additionally, there are other characteristics of the data that should be accounted for when calibrating a model, such as:
Stationarity: A time series is stationary if its overall behavior—such as average value, variability, and patterns—does not change over time. For example, the level of GDP is not stationary because its average value rises over time, but its differences (quartery change) are typically stationary.
Autocorrelation: Autocorrelation measures how strongly a value in the time series is related to its past values, helping identify patterns such as seasonality or repeated cycles.
Structural Breaks and Outliers: Structural breaks refer to sudden shifts in the trend or behavior of a time series (e.g., due to economic policy changes), while outliers are unusual spikes or drops that do not follow the typical pattern.
External Variables: These refer to other factors that have a relationship with the target variable. How strong is their correlation? Are they cointegrated?
The statsmodels package offers various tools to easiy test all of the above.
CLASSICAL TIME SERIES MODELS
The list of models that follows isn’t exhaustive, but these are some of the most popular and should be included in every forecaster’s toolkit.
These approaches will, at the very least, provide a useful baseline before exploring more sophisticated and computationally expensive techniques.1
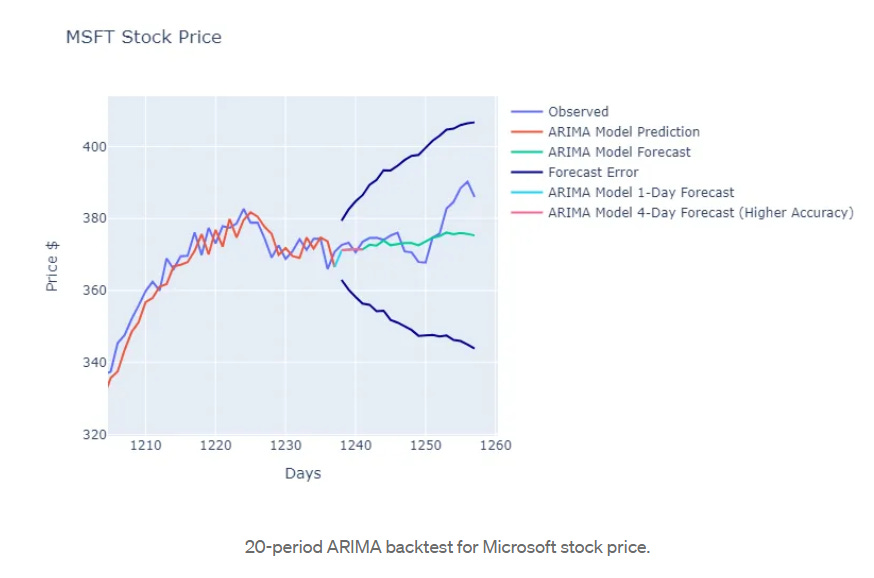
(1) ARIMA (Autoregressive Integrated Moving Average)
ARIMA is a flexible and popular time series model used to forecast data, especially in univariate settings, by combining three key components:
AR (Autoregressive): Models the relationship between the current value and its own past values (lags). The "order" of AR (p) determines how many past values the model uses.
I (Integrated): Handles non-stationary data by differencing the series to make it stationary. The "order" of differencing (d) determines how many times the data is differenced to remove trends.
MA (Moving Average): Models the relationship between the current value and past forecast errors (residuals). The "order" of MA (q) determines how many past error terms are included.
Imagine you want to predict the closing price of a stock each day and observe the following patterns:
The stock price exhibits momentum: Today’s price is often influenced by prices from the past few days, so p=2 (today’s price depends on prices from the last two days).
There is an upward trend, requiring d=1 (one differencing step to to transform the series into a stationary one and model the daily change in price).
Forecast errors from previous days seem to impact future prices: For instance, if you underpredicted the price yesterday, it might adjust upwards today, which is captured by q=1 (one moving average term where the last day’s forecast error affects today’s prediction).
In this scenario, you would specify the model as ARIMA(2, 1, 1).
In the statsmodels library, you can directly estimate this model using the ARIMA function.
from statsmodels.tsa.arima.model import ARIMA
model = ARIMA(stock_data['Close'], order=(2, 1, 1)) # ARIMA(p, d, q)
results = model.fit()There are several common statistical tests in the statsmodels library to help accurately determine the exact orders—checkout this tutorial.
If you’re feeling lazy, there’s even a function called auto_arima from the pmdarima package, which can determine the best orders for you with a single function. You can find an overview of the manual approach versus auto_arima here.
The beauty of ARIMA is its flexibility to mix and match its components. You can set p, d, and q to different orders, tailoring the model to your data.
Extensions: SARIMA, ARIMAX, and SARIMAX, incorporate seasonality (‘S’), external predictors (‘X’), or both, enabling you to handle more complex time series patterns and relationships.
(2) ARDL (Autoregressive Distributed Lag)
An ARDL model is an extension of Autoregressive (AR) models (the AR part of ARIMA) that combines lagged values of the dependent variable (autoregressive terms) with lagged values of one or more independent variables, along with seasonal dummies.
This is particularly useful when you want to extend your univariate AR model to include other explanatory variables. For example, a ARDL model for house prices might look something like this:
House Price Today = Constant+(Lag 1 House Price) + (Lag 2 House Price) + (Current Mortgage Rate) + (Lag 1 Mortgage Rate) + (Summer Dummy) + (Error Term)The convenient thing about the statsmodels package is that it can automatically determine the ideal lag orders for you and directly estimate your model.
For example, to forecast real consumption, you can use the ardl_select_order function, which suggests 5 lags of consumption and 1 lag of GDP. You can then use ardl.fit() to estimate the model.
from statsmodels.tsa.api import ARDL
from statsmodels.tsa.ardl import ardl_select_order
sel_res = ardl_select_order(
data.c, # Dependent variable (consumption)
8, # Maximum lag for the dependent variable
data[["g"]], # Independent variable(s) (gdp)
8, # Maximum lag for the independent variable(s)
trend="c", # Include a constant (intercept) term in the model
seasonal=True, # Account for seasonal components in the model
ic="aic", # Use the Akaike Information Criterion to select the best model
)
ardl = sel_res.model
ardl.ardl_order
-> (5, 1) # ideal lag orders
res = ardl.fit(use_t=True)Here’s how the model looks when we fit it with data up to 2000Q1 and predict the next four quarters.
The ARDL model has an advantage over ARIMA in that it can handle non-stationary data as well. This means it is capable of capturing both the short-term and long-term relationships between variables.
For example, the levels of house prices, household income, and housing investment tend to move together over time—house prices cannot grow endlessly while income remains stagnant2. In statistical jargon, these variables are said to be cointegrated.
In this case, the ARDL model can be modified into what is called an Error Correction Model (ECM), which accounts for short-term movements of each variable while also capturing additional dynamics when the variables deviate too far from one another.
ARDL allows the forecaster to impose more economic intuition into the model, rather than focusing solely on pure forecasting accuracy as in ARIMA.
(3) VAR (Vector Autoregression)
A VAR model captures the dynamic relationships among multiple interdependent variables by using each variable’s past values (lags) as predictors for all variables in the system.
Unlike ARDL, VAR models allow you to predict multiple variables within a system, such as GDP components or interrelated financial variables like exchange rates, interest rates, and bond yields. VAR is commonly used as a benchmark for macroeconomic forecasts before diving into more complex approaches.
The system of equations for a VAR model of real GDP, real consumption, and real investment with a lag order of 1 would look like this:
realgdp(t) = Constant for realgdp(t) + realgdp(t-1) + realcons(t-1) + realinv(t-1) + Error term for realgdp(t)
realcons(t) = Constant for realcons(t) + realgdp(t-1) + realcons(t-1) + realinv(t-1) + Error term for realcons(t)
realinv(t) = Constant for realinv(t) + realgdp(t-1) + realcons(t-1) + realinv(t-1) + Error term for realinv(t)statsmodels allows you to define the optimal lag order directly, or you can let it select the optimal lag order based on statistical criteria.
from statsmodels.tsa.api import VAR
# Automatically select the optimal lag order using AIC, considering up to 15 lags
model = VAR(data) # Initialize a VAR model with the dataset
results = model.fit(maxlags=15, ic='aic')
The fitted model can then be used for forecasting.

Another useful output of VAR models is impulse response functions, which show how a shock (unexpected change) to one variable in a VAR system affects all the variables in the system over time.
A common use case for this is estimating the impact of policy shocks on the economy, such as an interest rate hike by the central bank or an increase in government spending.

Extensions: VAR models can be extended to structural VAR (SVAR) and Vector Error Correction Models (VECM). They can also incorporate exogenous variables (VARX).3
(4) Exponential smoothing
Exponential smoothing is a time series forecasting technique that uses weighted averages of past observations, assigning higher weights to more recent data points.
The technique is essentially like drawing a smooth line through the data to eliminate short-term noise and projecting that line into the future.
There are three variations that can all be implemented with statsmodels:
Simple Exponential Smoothing (SES): Suitable for data without trends or seasonality.
Holt’s Linear Trend Method: Suitable for data with a trend but no seasonality.
Holt-Winters Exponential Smoothing: Ideal for data with both trends and seasonality.
Here, you can see the differences in forecasting airline passengers, where Holt-Winters (HW) best captures both the trend and seasonality.

The art with exponential smoothing lies in selecting the right smoothing parameters for each model. For example, with Simple Exponential Smoothing, statsmodels allows you to optimize the smoothing parameter (alpha) like so:
from statsmodels.tsa.api import SimpleExpSmoothing,
# The "estimated" initialization method is used to optimize the smoothing parameter
optimal_fit = SimpleExpSmoothing(oildata, initialization_method="estimated").fit()Below, we can see that the optimaly selected alpha of 0.89 provides a better fit for the oil production data.
Summary
Here is a quick recap of the models I just covered and their key strength:
ARIMA: Captures dependencies in univariate data with trends and seasonality by combining autoregression, differencing, and moving averages.
ARDL: Handles both short-term and long-term relationships between dependent and independent variables, even with non-stationary data.
VAR: Models the interdependence between multiple variables, making it ideal for systems like macroeconomic indicators.
Exponential Smoothing: Provides a simple and effective method for smoothing data and projecting trends, especially when combined with extensions like Holt-Winters for seasonal patterns.
All of these models serve as excellent starting points for most time-series prediction problems, and statsmodels makes it straightforward to implement them in Python.
I’ll be sharing step-by-step examples in follow-up posts to demonstrate how to make such models operational in real-world scenarios.
This guide assumes that the reader has a basic understanding of ordinary least squares (OLS) regression and statistics.
Here’s a research paper from the European Central Bank using an ECM for housing dynamics.
For more details on these, refer to the statsmodels documentation.